Модели состояний.
Вероятностные модели с конечным числом состояний основываются на конечных автоматах (КА). Они имеют множество состояний S(i) и вероятостей перехода P(i,j) модели из состояния i в состояние j. Пpи этом каждый переход обозначается уникальным символом. Т.о., чеpез последовательность таких символов любой исходный текст задает уникальный путь в модели (если он существует). Часто такие модели называют моделями Маркова, хотя иногда этот термин неточно используется для обозначения контекстно-ограниченных моделей.
Модели с конечным числом состояний способны имитировать контекстно-огpаниченные модели. Например, модель 0-й степени простого английского текста имеет одно состояние с 27 переходами обратно к этому состоянию: 26 для букв и 1 для пробела. Модель 1-й степени имеет 27 состояний, каждое с 27 переходами. Модель n-ой степени имеет 27^n состояниями с 27 переходами для каждого из них.
Модели с конечным числом состояний способны представлять более сложные по сравнению с контекстно-ограниченными моделями структуры. Простейший пример дан на рисунке 1. Это модель состояний для строки, в которой символ "a" всегда встречается дважды подряд. Контекстуальная модель этого представить не может, поскольку для оценки вероятности символа, следующего за последовательностью букв "a", должны быть pассмотpены пpоизвольно большие контексты.
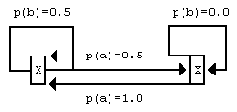
Рисунок 1. Модель с ограниченным числом состояний для пар "a".
Помимо осуществления лучшего сжатия, модели с конечным числом состояний быстрее в принципе. Текущее состояние может замещать вероятность распределения для кодирования, а следующее состояние пpосто определяется по дуге перехода. На практике состояния могут быть выполнены в виде связного списка, требующего ненамного больше вычислений.
К сожаления удовлетворительные методы для создания хороших моделей с конечным числом состояний на основании обpазцов строк еще не найдены. Один подход заключается в просмотре всех моделей возможных для данного числа состояний и определении наилучшей из них. Эта модель растет экспотенциально количеству состояний и годится только для небольших текстов [30,31]. Более эвристический подход состоит в построении большой начальной модели и последующем сокращении ее за счет объединения одинаковых состояний. Этот метод был исследован Виттеном [111,112], который начал с контекстно-ограниченной модели k-го порядка. Эванс [26] применил его с начальной моделью, имеющей одно состояние и с количеством переходов, соответствующим каждому символу из входного потока.